

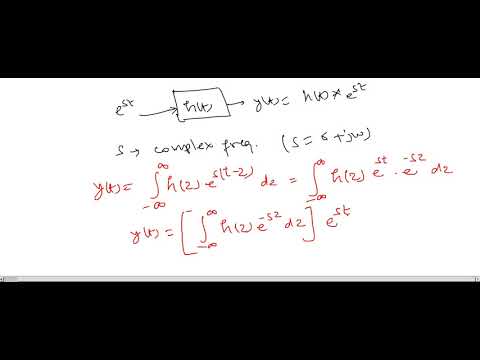
A system represented by the following imput-output equation is nonlinear: y(t) x2(t) Let x(t). Consider the cases of nonlinear and of time varying systems.
#EIGENFUNCTION PROPERTY OF LTI SYSTEMS SERIES#
2: A x b where x and b are in C n and A is an N ×. This video playlist deals with Continuous Time Fourier Series (CTFS) theory, mathematical expressions and problems.Please watch the complete playlist to get. is mathematically analogous to an N × N matrix A operating on a vector x C N to produce another vector b C N (see Matrices and LTI Systems for an overview). The problem is that practical LTI systems are not boundless nor are they acausal. The eigenfunction property is only valid for LTI systems. f and t are continuous time (CT) signals and H is an LTI operator. Mathematically (and theoretically), there is no need for the exponential function to be a complex sinusoid. 4 The eigenfunctions k(t)and their properties (Focus on CT systems now, but results apply to DT systems as well.) eigenvalue eigenfunction Eigenfunction in. We can readily prove this eigenfunction property in general for an arbitrary ( not necessarily causal ) LTI system using the superposition integral.


 0 kommentar(er)
0 kommentar(er)
